25.3. Implementing Locks

Now let’s try to implement the lock data type. In the following examples, we will use C/C++-like pseudo-code, rather than actual C, to make the key points more clearly. We will also consider the special case of two concurrent threads first, before the general case of N concurrent threads.

25.3.1. The Oldest Trick in the Book - Disable Interrupts

Earlier, we blamed interrupts for causing untimely context switches that allowed thread operations to be interleaved arbitrarily. So, if we disable interrupts in the acquire() function before the critical section, the currently executing thread cannot be kicked off the CPU until it enables interrupts in the release() function. Alas, this enticingly simple solution won’t work in most cases. First, user-level processes are not allowed to disable interrupts, so this solution is only available to operating system code. Second, leaving interrupts disabled for a long period of time can cause other problems, so even in the OS, it can only be used for short critical sections that do not cause blocking. Third, we can’t have different locks protecting different shared data objects if locks are implemented by disabling interrupts, since this approach will prevent other threads from running at all, regardless of what data they might want to access. Finally, and perhaps most importantly, disabling interrupts offers no protection against concurrent accesses from a thread running on another CPU, so this solution can only be applied on a uniprocessor. Historically, disabling interrupts was used to protect short critical sections in OS code, but in the multicore era, this idea has very limited uses.

Listing 25.7 Lock implementation using using interrupt disabling; C++-like definition.

struct lock {

    void acquire() {
        disable_interrupts(); // cli on x86
    }

    void release() {
        enable_interrupts(); // sti on x86
    }
}

We now consider more general solutions that can be used in either user-level programs, or the operating system, without relying on any special hardware assistance.

25.3.2. Lock Implementation Attempts with Ordinary Machine Instructions

In this section, we will show you several attempts at implementing the lock functions that encapsulate the critical section entry and exit protocols. All of these solutions (or solution attempts) use only ordinary machine instructions (load, store, cmp, jmp, add, etc.).

25.3.2.1. (Broken) Lock Implementation Attempt #1 - Check a Flag

Suppose we introduce a shared boolean variable to check if the critical section is currently in use, as shown in Listing 25.8.

Listing 25.8 Lock implementation using a flag; C++-like definition.

struct lock_s {
    bool locked = false;
    
    void acquire() {
        while(locked) { }; // empty loop body, just spins
        locked = true;
    }

    void release() {
        locked = false; 
    }
}

Each thread will check the locked flag repeatedly in the while() loop of the acquire() function until it finds the critical section is free. When a thread breaks out of the loop, it sets the locked flag to true, preventing other threads from accessing the critical section until it is done. On exit, it sets the locked flag to false again in the release() function so that another thread can enter.

This is called a spinlock because threads spin around the while loop until they can gain entry to the critical section. Since a thread keeps the CPU busy while it is waiting for entry, this spinning is called busy waiting.

Alas, this does not meet the mutual exclusion requirement. We have just replaced one race with another. Consider two concurrent threads, T0 and T1, attempting to enter their critical sections concurrently by calling acquire() on the same lock object. Each thread tests the value of locked, sees that is is false, and breaks out of their respective while loops. Both T0 and T1 then set locked=true and proceed to enter their critical sections concurrently. The mutual exclusion requirement is violated, so we will have to try again.

The heart of the problem with this non-solution is that our threads’ operations can interleave so that the locked flag can change between the time when a thread tests if it is safe to proceed and the time when the thread sets the flag to prevent others from also entering the critical section. If we could make the TEST and the SET an indivisible atomic operation, this problem would go away. Indeed, today’s processor architectures give us an instruction with the properties we need. But, the processors of the Djikstra’s era did not, and it is instructive to consider how we can implement the critical section entry and exit protocols without special assistance from the hardware. We will then see how some hardware support simplifies matters considerably.

25.3.2.2. (Broked) Lock Implementation Attempt #2 - Take Turns

Let’s try replacing the boolean flag with a turn variable to indicate which thread is allowed to use the critical section. Each thread will wait for turn to be set to its own thread id (tid) in the acquire() function before entering, and will set turn to the other thread’s id in the release() function when it is done using the critical section, as shown in Listing 25.9.

Listing 25.9 Lock implementation for two threads using turns; C++-like definition.

struct lock_s {
    int turn = 0;
    
    void acquire() {
        int me = getTid(); // which thread is running this function? Threads are numbered 0 or 1.
        while(turn != me) { }; // empty loop body, just spins
    }

    void release() {
        int me = getTid();
        turn = 1 - me; // set turn to other thread (if me == 0, turn = 1; if me == 1, turn = 0)
    }
}

Does this meet our requirements? Let’s examine them one by one.

Mutual exclusion

The value of turn can only be 0 or 1 at any instant in time, and only the thread whose id matches turn is allowed entry to the critical section. So mutual exclusion is satisfied.

Progress

This requirement has two parts. The first part says that we can’t delay the decision of which thread next gets to enter the critical section forever. That part is fine — we decide on the next thread in the release() function by flipping the turn variable. The second part of the progress requirement says that threads in their remainder code can’t delay threads that want to use the critical section, and here lies the problem. This solution requires a strict alternation of threads in the critical section. In Listing 25.9 we initialized turn so that T0 must go first, but T0 and T1 could have different tasks and run at different relative speeds. If T1 reaches its critical section first, it is still blocked until T0 goes through its critical section and flips turn to 1. Similarly, if one thread has less work to do, and needs fewer trips through the critical section, it could leave the other thread waiting indefinitely for another turn.

Bounded waiting

Strangely, this does satisfy bounded waiting, since there is a bound on the number of times other threads can use the critical section after a thread has started the entry protocol (i.e., after a thread has invoked the acquire() function). Threads take turns, so T0 can use the critical section at most once after T1 calls the acquire() function and before T1 gains entry. It is irrelevant though because we don’t have Progress.

The issue with this “solution” is that a thread must wait its turn, even when the other thread has no interest in entering its critical section.

We could go on for quite some time showing you attempts at solutions that do not quite work. In his classic 1965 paper on “Cooperating Sequential Processes” [Dij65], Djikstra lays out several other broken alternatives and admits that “people that had played with the problem started to doubt whether it could be solved at all.” He gives credit to Dutch mathematication T. J. Dekker for coming up with the first correct solution for two threads (in 1959!). The main idea is to combine the notion of turns with an expression of interest from a thread when it wants to enter its critical section. You can read all about [Dekker’s Algorithm]https://en.wikipedia.org/wiki/Dekker%27s_algorithm elsewhere, but suffice to say that it was fairly complex and doesn’t generalize to more than two threads. A simpler solution that can generalize to more than 2 threads, built on the same ideas of combining turns with expressions of interest, was published by Gary L. Peterson in 1981 [Pet81].

25.3.2.3. Lock Implementation Attempt #3 - Peterson’s Algorithm

The code for Peterson’s Algorithm is shown in Listing 25.10. We have added an array of boolean flags, interested where each thread can indicate its interest in entering its critical section, and initially both flags are set to false. Each thread will only write to its own interested flag, and read from the other thread’s interested flag. To gain entry to its critical section, a thread first sets its interested flag to true so that the other thread can see that it wants to enter. Then, it will politely set the turn to the other thread, and busy wait until it sees that either the other thread is not interested, or the other thread has given back the turn. To leave the critical section, a thread simply sets its interested flag to false.

Listing 25.10 Lock implementation for two threads using Peterson’s Algorithm; C++-like definition.

struct lock_s {
    int turn = 0;
    bool interested[2] = {false; false};
    
    void acquire() {
        int me = getTid(); // which thread is running this function? Threads are numbered 0 or 1.
        int other = 1 - me; // other thread's id
        
        interested[me] = true; // this thread wants to enter the critical section
        turn = other;          // but is giving the other thread a chance to go first
        while(interested[other] == true && turn == other) { }; // empty loop body, just spins
        
    }

    void release() {
        int me = getTid();
        interested[me] = false;
    }
}

Let’s see if this solution meets all of our requirements.

Mutual Exclusion

The combination of interested and turn variables ensure that only one thread can be in the critical section at a time. Suppose both T0 and T1 try to enter their critical sections at nearly the same time by calling acquire(). Both set their interested flags to true, so now both threads can see that the other thread is trying to enter. Now, both threads set turn to the other thread’s id—either T0 setting turn = 1 takes effect first and is overwritten by T1 setting turn = 0, or vice versa. Only one thread will be able to exit the while loop, because turn must be either 0 or 1. Suppose T0 is already in the critical section when T1 calls acquire(), then interested[0] == true and turn == 1, and T1 must wait in the while loop until interested[0] becomes false, which only happens when T0 leaves the critical section by calling release().

Progress

The second part of the progress requirement (threads in their remainder code do not delay threads that want to enter the critical section) is satisfied because the interested flag is false for any thread in the remainder code, and a thread can enter when interested[other] == false. The first part of the progress requirement (threads that want to enter can eventually do so) is satisfied because once a thread \(T_i\) calls acquire() it will eventually return. There are only three possibilities. (1) if the other thread, \(T_j\), is not interested in using the critical section, then interested[other] == false and \(T_i\) can exit the while loop immediately and enter the critical section. (2) if the other thread, \(T_j\), is already in its critical section, then interested[other] will eventually become false when \(T_j\) leaves its critical section, and \(T_i\) can exit its while loop and enter. (3) The other thread, \(T_j\) is also requesting entry to its critical section, and must set turn to \(T_i\) after setting its own interested flag; \(T_i\) will exit its while loop because turn == other is now false, and \(T_i\) can enter the critical section.

Bounded Waiting

Once a thread \(T_i\) has indicated interest in entering the critical section, the other thread \(T_j\) can enter at most once before \(T_i\) is granted entry, because \(T_j\) must set turn to \(T_i\) when it tries to enter again.

We have made an informal argument that Peterson’s Algorithm satisfies the requirements. You should be skeptical of such arguments, because the history of synchronization teaches us that informal correctness arguments about concurrency are often wrong. The interested reader can find formal proofs of the correctness of Peterson’s algorithm [Sch97], or you can take our word for it.

25.3.2.4. Discussion

Over the years, many other algorithms were developed to solve the critical section problem, relying only on ordinary machine instructions. However, simpler solutions exist if we take advantage of special atomic machine instructions that are provided by all modern processor architectures. In addition, modern CPUs may re-order instructions on-the-fly during execution, and allow threads running on different CPUs to observe the effects of memory operations in different orders (this is called a relaxed memory consistency model but it can cause a lot of stress for programmers!). To make the solutions in this section work on modern hardware, additional instructions called fences have to be added to ensure correctness. We might as well use atomic instructions in the first place.

25.3.3. Atomic Instructions for Synchronization

Recall that we ran into trouble with our first lock implementation in Section 25.3.2.1, because threads could have their execution interrupted and interleaved with another thread also running the acquire() function between testing the locked flag and setting it to true. In this section we will look briefly at the semantics of some atomic machine instructions that can help us solve this problem.

25.3.3.1. Test-and-Set (TAS)

Some CPU architectures provide an atomic test-and-set instruction with the behavior shown in Listing 25.11. Keep in mind that this code is just to show the effect of the test-and-set instruction — it is really a single operation that executes atomically.

Listing 25.11 Semantics of the test-and-set atomic instruction.

bool test-and-set(bool *location) 
{
    bool old = *location;
    if (old == false)
        *location = true;    
    return old;
}

Notice that the value stored at location is always true after executing test-and-set — either it was already true at the start, or it was initially false, the test succeeded, and it was set to true. By examining the old value, we can tell which case occurred. Actual implementations may make the test implicit and just unconditionally set *location = true, as shown in Listing 25.12:

Listing 25.12 Semantics of the test-and-set atomic instruction, alternate implementation.

bool test-and-set(bool *location) 
{
    bool old = *location;
    *location = true;    
    return old;
}

Armed with a test-and-set instruction, implementing a lock is very easy.

Listing 25.13 Lock implementation using test-and-set; C++-like definition.

struct lock {
    bool locked = false;
    
    void acquire() {
        while(test-and-set(&locked)) { }; // empty loop body, just spins
    }

    void release() {
        locked = false; 
    }
}

In the acquire() function, a thread will atomically check the state of the locked variable and set it to true. If the critical section is already in use by another thread, then locked will be true already, test-and-set will return true and the thread will stay in the while loop and try again. Eventually, the other thread will leave the critical section and call release(), setting locked to false. The next test-and-set will return false as the old value of locked (and will set locked to true), and the thread will leave the while loop and enter the critical section. But what if locked is false and two threads try to enter the critical section at the same time? Because test-and-set is atomic, one of the thread’s will execute the instruction first and succeed in setting locked to true, while the other thread will fail and be forced to retry. Thus, the mutual exclusion requirement is met.

25.3.3.2. Compare-and-Swap (CAS)

Another common atomic instruction is compare-and-swap, or CAS, which has the semantics shown in Listing 25.14.

Listing 25.14 Semantics of the compare-and-swap instruction.

bool compare-and-swap(int *location, int expected, int newval) 
{
    if (*location != expected) 
        return false;
        
    *location = newval;
    return true;
}

We can also implement locks using the compare-and-swap atomic operation.

Listing 25.15 Lock implementation using compare-and-swap; C++-like definition.

struct lock {
    bool locked = false;
    
    void acquire() {
        while(!compare-and-swap(&locked, false, true)) { }; // empty loop body, just spins
    }

    void release() {
        locked = false; 
    }
}

This is essentially the same as the version using test-and-set. A thread wanting to enter the critical section atomically compares the current value of locked to false. As long as the critical section is unavailable, this comparison will fail, compare-and-swap returns false, and the thread has to stay in the while loop trying again.

25.3.3.3. Are the Requirements Met?

We have already argued that these spinlocks using atomic test-and-set or compare-and-swap meet the Mutual Exclusion requirement. It should be clear that the Progress requirement is also met, since some thread can successfully enter the critical section as soon as the lock is released, and no remainder code can have any influence over this, since the value of the locked flag is only accessed inside the acquire() and release() functions. But what about Bounded Waiting? Unfortunately, an “unlucky” thread might always try its test-and-set at an instant when the locked flag has been set to true by another thread, continually retrying while other threads enter and leave the critical section an unlimited number of times, so we don’t have Bounded Waiting with these lock implementations. We show this unfortunate possibility in Fig. 25.4.

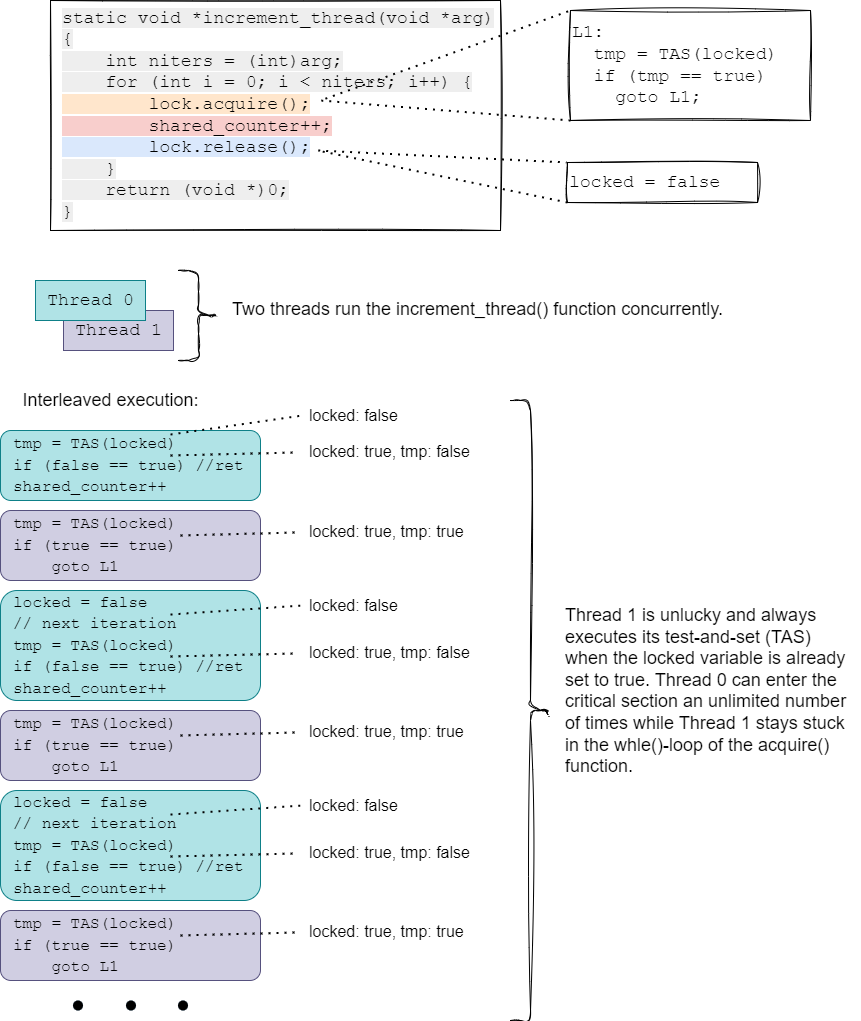
Fig. 25.4 Starvation is possible with simple test-and-set spinlocks.

Although we have illustrated the issue using test-and-set, exactly the same problem can arise when spinlocks are implemented using compare-and-swap.

25.3.3.4. Atomic Instructions and Portability

Different processor architectures provide different atomic instructions, making our lock implementations non-portable. However, the machine-dependent code can be hidden by library implementations. We also simplified the implementations that we showed you in Listing 25.13 and Listing 25.15 by ignoring the need for fences in the release() function. And, we ignored the fact that C compilers can optimize accesses to plain variables, like locked, in ways that break correctness in the face of multi-threading.

It wasn’t until C11/C++11 that the C programming language got a memory consistency model and standard, language-level support for atomic operations. Now, it is possible to write portable versions of the lock functions, with the C compiler translating the atomic operations into the correct machine instructions for the target architecture. We show a portable C11 implementation of a spinlock using test-and-set in Listing 25.16.

Note

There are also atomic versions of simple arithmetic instructions, like add, which we would prefer to use for a simple operation like incrementing the shared counter. Most critical sections in real code are much more complex (we will see a few examples soon).

Listing 25.16 spinlock.h - Basic spinlock using C11 atomics.

#include <stdatomic.h>

typedef struct spinlock_s {
    atomic_flag locked;
} spinlock_t; 

static inline void spinlock_init(spinlock_t *l) {
    atomic_flag_clear( &l->locked );
}

static inline void spinlock_acquire(spinlock_t *l)
{
    while(atomic_flag_test_and_set( &l->locked )) { };
}

static inline void spinlock_release(spinlock_t *l)
{
    atomic_flag_clear( &l->locked );
}

We argued earlier that a test-and-set spinlock ensures mutual exclusion and progress. Now, let’s see it in action by replacing the pthread_mutex in our shared counter example program with this spinlock implementatioin. The code is shown in Listing 25.17.

Listing 25.17 counter_spinlock.c - shared counter example using test-and-set spinlock to protect access to counter variable.

#include <pthread.h>
#include <stdlib.h>
#include <sys/types.h>
#include <unistd.h>
#include <string.h>
#include <stdio.h>
#include "spinlock.h"

spinlock_t splock;
volatile long shared_counter;

static void *increment_thread(void *arg)
{
    long niters = (long)arg;
    for (int i = 0; i < niters; i++) {
        spinlock_acquire(&splock);
        shared_counter++;
        spinlock_release(&splock);
    }

    return (void *)0;
}

static void *decrement_thread(void *arg)
{
    long niters = (long)arg;

    for (int i = 0; i < niters; i++) {
        spinlock_acquire(&splock);
        shared_counter--;
        spinlock_release(&splock);
    }

    return (void *)0;
}

int main(int argc, char **argv)
{
    pthread_t *tids;
    long niters;
    int nthreads, i;
    
    if (argc != 3) {
        fprintf(stderr,"Usage: %s <num_threads> <num_iters>\n",argv[0]);
        return 1;
    }

    nthreads = atoi(argv[1]);
    niters = atoi(argv[2]);
    shared_counter = 0;
    spinlock_init( &splock );
    
    printf("Main thread: Beginning test with %d threads\n", nthreads);
    
    tids = (pthread_t *)malloc(nthreads * sizeof(pthread_t));
    
    /* We create the same number of increment and decrement threads, each doing the same number of iterations. 
     * When all threads have completed, we expect the final value of the shared counter to be the same as its
     * initial value (i.e., 0).
     */
    for (i = 0; i < nthreads; i+=2) {
        (void)pthread_create(&tids[i], NULL, increment_thread, (void *)niters );
        (void)pthread_create(&tids[i+1], NULL, decrement_thread, (void *)niters );
    }
    
    /* Wait for child threads to finish */
    for (i = 0; i < nthreads; i+=2) {
        pthread_join(tids[i], NULL);
        pthread_join(tids[i+1], NULL);
    }
    
    printf("Main thread: Final value of shared counter is %ld\n", shared_counter);

    return 0;
}

As you can see, the final value of the shared counter is always 0, as expected. (This kind of testing can’t prove that our implementation is correct, but it can reveal when our implementation is incorrect.)

Next, we turn our attention to the final requirement, bounded waiting. This can also be expressed as a fairness requirement—every thread should have an equal chance to acquire a lock and enter its critical section.

25.3.3.5. Ticket Locks

How unfair are plain spinlocks?

It turns out they can be quite unfair indeed. When ticket locks were introduced to the Linux kernel, the patch description included this motivation for them:

On an 8 core (2 socket) Opteron, spinlock unfairness is extremely noticable, with a userspace test having a difference of up to 2x runtime per thread, and some threads are starved or “unfairly” granted the lock up to 1 000 000 (!) times. After this patch, all threads appear to finish at exactly the same time.

---Nick Piggin, [LKML 2007]

Mellor-Crummey and Scott introduced ticket locks as a simple way to achieve bounded waiting using an atomic fetch-and-add (FAA) machine instruction [MCS91]. (The fetch-and-add instruction has the semantics shown in Listing 25.18.) They observed that ticket locks could be viewed as an optimization of Lamport’s classic Bakery Algorithm [Lam74]. To understand how ticket locks work, imagine a bakery with a ticket dispenser and a display behind the counter showing the ticket number of the next customer to be served. Customers take a ticket when they come into the bakery, and wait until the display shows their number. Customers are served in the order they claim their tickets, so we can guarantee no starvation.

Listing 25.18 Semantics of the fetch-and-add atomic instruction; atomically increments the contents of a memory location by a specified value, returning the previous contents of the memory location.

int fetch_and_add(int *location, int value)
{
    int tmp = *location;
    *location = tmp + value;
    return tmp;
}

To use this idea in a lock data type, we need two counters, next_ticket and now_serving. To acquire the lock, a thread first gets a ticket and increments the next_ticket variable, using the atomic fetch-and-add instruction. Because fetch-and-add is an indivisible machine instruction, each thread is guaranteed a unique ticket number. To wait for its turn, a thread simply spins testing to see if the now_serving variable matches its ticket. When that happens, the thread breaks out of the while loop, and enters its critical section. To release the lock, a thread simply increments the now_serving variable, which will allow exactly one thread (the one holding the next ticket number) to acquire the lock next. We show an example of this implementation in Listing 25.19. Note that we do not need to use the fetch-and-add atomic instruction to increment now_serving in the release() function, because only the thread that acquired the lock can release it, and we don’t care about the previous value. On any real processor, however, we do need to worry about instruction reordering so we would need a memory fence in the release function.

Listing 25.19 Ticket lock implementation; C++-like definition.

struct lock {
    unsigned long next_ticket = 0;
    unsigned long now_serving = 0;
    
    void acquire() {
        unsigned long my_ticket = fetch_and_increment(&next_ticket, 1);
        while(my_ticket != now_serving) { }; // empty loop body, just spins
    }

    void release() {
        now_serving++; 
    }
}

In Listing 25.20, we show a portable, C11 implementation of a ticket lock.

Listing 25.20 C11 implementation of a ticket lock

#include <stdatomic.h>

typedef struct ticketlock_s {
    atomic_ulong next_ticket;
    atomic_ulong now_serving;
} ticketlock_t; 

static inline void ticketlock_init(ticketlock_t *l) {
    l->next_ticket = 0;
    l->now_serving = 0;
}

static inline void ticketlock_acquire(ticketlock_t *l)
{
    unsigned long my_ticket = atomic_fetch_add(&l->next_ticket, 1);
    while(my_ticket != l->now_serving) { };
}

static inline void ticketlock_release(ticketlock_t *l)
{
    l->now_serving++;
}

Now, let’s see the ticket lock in action by replacing the previous spinlock in our shared counter example program with this ticketlock implementatioin. The code is shown in Listing 25.21.

Listing 25.21 counter_ticketlock.c - shared counter example using ticket lock to protect access to counter variable.

#include <pthread.h>
#include <stdlib.h>
#include <sys/types.h>
#include <unistd.h>
#include <string.h>
#include <stdio.h>
#include "ticketlock.h"

ticketlock_t tktlock;
volatile long shared_counter;

static void *increment_thread(void *arg)
{
    long niters = (long)arg;
    for (int i = 0; i < niters; i++) {
        ticketlock_acquire(&tktlock);
        shared_counter++;
        ticketlock_release(&tktlock);
    }

    return (void *)0;
}

static void *decrement_thread(void *arg)
{
    long niters = (long)arg;

    for (int i = 0; i < niters; i++) {
        ticketlock_acquire(&tktlock);
        shared_counter--;
        ticketlock_release(&tktlock);
    }

    return (void *)0;
}

int main(int argc, char **argv)
{
    pthread_t *tids;
    long niters;
    int nthreads, i;
    
    if (argc != 3) {
        fprintf(stderr,"Usage: %s <num_threads> <num_iters>\n",argv[0]);
        return 1;
    }

    nthreads = atoi(argv[1]);
    niters = atoi(argv[2]);
    shared_counter = 0;
    ticketlock_init( &tktlock );
    
    printf("Main thread: Beginning test with %d threads\n", nthreads);
    
    tids = (pthread_t *)malloc(nthreads * sizeof(pthread_t));
    
    /* We create the same number of increment and decrement threads, each doing the same number of iterations. 
     * When all threads have completed, we expect the final value of the shared counter to be the same as its
     * initial value (i.e., 0).
     */
    for (i = 0; i < nthreads; i+=2) {
        (void)pthread_create(&tids[i], NULL, increment_thread, (void *)niters );
        (void)pthread_create(&tids[i+1], NULL, decrement_thread, (void *)niters );
    }
    
    /* Wait for child threads to finish */
    for (i = 0; i < nthreads; i+=2) {
        pthread_join(tids[i], NULL);
        pthread_join(tids[i+1], NULL);
    }
    
    printf("Main thread: Final value of shared counter is %ld\n", shared_counter);

    return 0;
}

25.3.3.6. Comparing Lock Implementations

Test-and-set spinlocks, ticket locks, or the mutex from the pthreads library (pthread_mutex_t) can all provide mutual exclusion and ensure progress, but ticket locks can guarantee fairness, unlike test-and-set spinlocks. On the other hand, you can see that more work is required to acquire and release a ticket lock. To see how these implementations stack up, we have a very simple test program that creates some number of threads and has each thread count the number of times it can acquire and release the lock in a fixed amount of time. The parent thread sets a global flag to allow the children to start counting after all the threads have been created, sleeps for some amount of time, and then sets another global flag to tell the children to stop. Once all the child threads are done, the parent reports on the total number of iterations completed by all children, and the difference between the most and least productive thread. This program for the test-and-set spinlock is shown in Listing 25.22; we also have versions that replace the spinlock with a ticket lock, and with a pthread mutex.

Listing 25.22 check_spinlock_fairness.c - Sample program to show fairness and efficiency of test-and-set spinlock implementation.

#include <pthread.h>
#include <stdlib.h>
#include <sys/types.h>
#include <unistd.h>
#include <string.h>
#include <stdio.h>
#include <stdbool.h>
#include <limits.h>
#include "spinlock.h"

spinlock_t splock;
atomic_bool start;
atomic_bool done;

struct thread_info {
    pthread_t tid;
    unsigned iters_done;
};

static void *thread_func(void *arg)
{
    struct thread_info *my_info = (struct thread_info *)arg;
    unsigned i = 0;
    
    while(!start) {} ; /* Wait until parent flags that all threads have been created */ 
    
    while (!done) {
        spinlock_acquire(&splock);
        i++;
        spinlock_release(&splock);
    }

    my_info->iters_done = i;
    return (void *)0;
}



int main(int argc, char **argv)
{
    struct thread_info *tinfo;
    int duration;
    int nthreads, i;
    
    if (argc != 3) {
        fprintf(stderr,"Usage: %s <num_threads> <duration>\n\t where duration is the number of seconds for threads to run.\n",argv[0]);
        return 1;
    }

    start = false;
    done = false;
    nthreads = atoi(argv[1]);
    duration = atoi(argv[2]);
    spinlock_init( &splock );
    
    printf("Main thread: Beginning test with %d threads, running for %d seconds\n", nthreads, duration);
    
    tinfo = (struct thread_info *)calloc(nthreads, sizeof(struct thread_info));

    /* We create the requested number of threads, all doing the same work */
    for (i = 0; i < nthreads; i++) {
        (void)pthread_create(&tinfo[i].tid, NULL, thread_func, (void *)&tinfo[i] );
    }
    
    /* All threads created. Let them run concurrently for requested duration. */
    start = true;
    sleep(duration);
    done = true;
    
    /* Wait for child threads to finish */
    for (i = 0; i < nthreads; i++) {
        pthread_join(tinfo[i].tid, NULL);
    }

    unsigned min_iters = UINT_MAX;
    unsigned max_iters = 0; 
    unsigned tot_iters = 0;
    for (i = 0; i < nthreads; i++) {
        tot_iters += tinfo[i].iters_done;
        if (tinfo[i].iters_done < min_iters) {
            min_iters = tinfo[i].iters_done;
        }
        if (tinfo[i].iters_done > max_iters) {
            max_iters = tinfo[i].iters_done;
        }
        printf("Thread %d completed %u iters\n", i, tinfo[i].iters_done);
    }
    
    unsigned diff = max_iters - min_iters;
    printf("\nTOTAL: %u iterations completed.\n", tot_iters);
    printf("Unfairness: Most productive thread completed %u iters, least productive thread completed %u iters\n", max_iters, min_iters);
    printf("Difference is %u iters\n", diff); 

    return 0;
}

Let’s compare the result of running the check_spinlock_fairness, check_ticketlock_fairness and check_mutex fairness programs on the container used to build this book. In each case, we start six threads and let them run for 5 seconds.

We’ll start with the test-and-set spinlock:

Actual numbers will vary from one trial to the next, but you should see somewhere around 12 million total iterations (~2 million iterations per thread on average), with a difference of a few hundred thousand iterations between the thread that did the most iterations, and the one that did the fewest. We often see the “fastest” thread performing 1.5x the work of the “slowest” thread.

Now, let’s look at the ticket lock:

You should see that the total number of iterations completed is somewhat smaller than with the test-and-set spinlock, reflecting the higher overhead of acquiring and releasing a ticket lock, with each thread completing around 1.9 million iteration on average. In exchange for this higher overhead, however, we get greater fairness, with a difference of less than 5,000 iterations between the “fastest” and “slowest” threads.

Finally, let’s see how the pthread library’s mutex implementation compares:

Two things should be readily apparent from these results. First, the pthreads mutex is much more efficient than our simple lock implementations, completing nearly twice as many iterations, with an average of nearly 4 million iterations per thread. Second, the pthreads mutex is fairer than the test-and-set spinlock, but less fair than the ticket lock, with the “fastest” thread completing ~1.15x more iterations than the “slowest” thread.

25.3.4. Sleep and Wakeup

We can build better spinlocks that are more efficient than the simple implementations we have shown and still satisfy the bounded waiting requirement, but we can’t get away from the fundamental problem of busy waiting. On a uniprocessor, busy waiting wastes precious CPU time. If a lock is not available the first time a thread tries to acquire it, the lock can’t possibly become available until the thread holding the lock gets a chance to run. So, the waiting thread will spin through its timeslice until the scheduler preempts it and switches to another thread. On a multiprocessor, it might be acceptable to spin while waiting for a lock if critical sections are short, since the lock could be released by a thread running on another CPU. Even on a multiprocessor, however, spinning can waste a lot of CPU time when critical sections are long, or when many threads are competing to acquire the lock. But what alternative do we have? One option is for the waiting thread to voluntarily yield the remainder of its timeslice when it can’t acquire a lock (e.g., via the sched_yield() system call). This helps, but can still have unnecessary overhead if the thread holding the lock is blocked (e.g., waiting for terminal input). In such cases, the scheduler will keep switching back to the thread trying to acquire the lock, which will keep yielding, until eventually the lock holder can run and release the lock. What we really want is a way to block a thread that is trying to acquire a lock until there is a chance that the lock is available, and then unblock a waiting thread when the lock is released. To that end, we introduce the following operations:

• sleep(wait_queue): blocks the calling thread; thread is added to wait_queue and another thread is selected to run.

• wakeup(wait_queue): removes a thread from wait_queue and adds it to the scheduler Ready queue.

• wakeup_all(wait_queue): moves all threads from wait_queue to the the scheduler Ready queue.

The wait_queue is simply a data structure that can keep track of the blocked threads. A simple implementation might be a linked list of thread ids that can be used to look up the corresponding thread. We will assume the list is kept in FIFO order, so that the thread that has been waiting the longest will be the first to wake up.

Unfortunately, this solution to the busy waiting problem just introduced another shared data structure (the wait_queue) and the steps to add or remove threads from the wait_queue are themselves critical sections. It looks like we’ve circled back to the same problem we started with. Fortunately, the operations to add or remove threads from a queue are short, so we can fall back on a spinlock to protect the wait_queue data structure and implement a sleep lock.